-
투영 행렬 유도하기이러저런 이야기 2019. 12. 19. 10:45
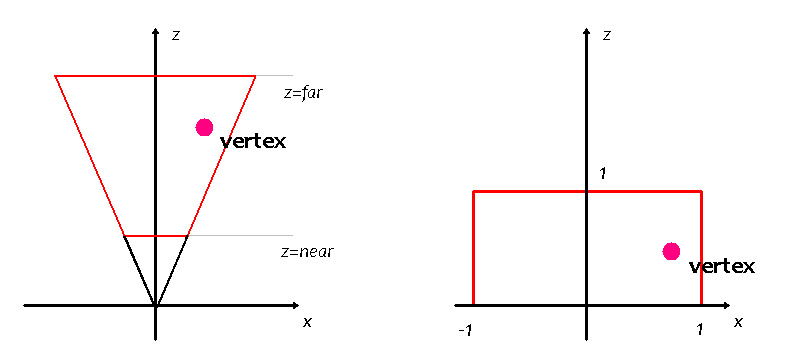
투영 변환이란 왼쪽 그림에서 보는 것 처럼 빨간색 영역은 카메라가 비출수있는 공간이다. z=near 가 근평면, z=far 가 원평면이라 하는데 카메라의 시야각에 따라 이 공간은 달라진다. 이 공간을 오른쪽에 보이는 그림과 같은 공간으로 변환 하는 것을 투영 변환이라 한다. 그림과 같이 모니터 화면을 가로, 세로의 크기가 2인 사각형으로 정규화시켜 작업하는데, 이렇게 정규화된 좌표계를 NDC(Normalized Device Coordinate)라고 한다. NDC는 변환되면 다음과 같이 가로, 세로의 크기가 2인 좌표 시스템을 가진다.

뷰스페이스의 점 P(x,y,z) 를 (-1,-1,0) ~ (1,1,1) 로 표현되는 공간상의 점 Q(X, Y, Z) 로 변환한다고 할 때 점P의 x가 점Q의 X로 변환되는 과정을 보면
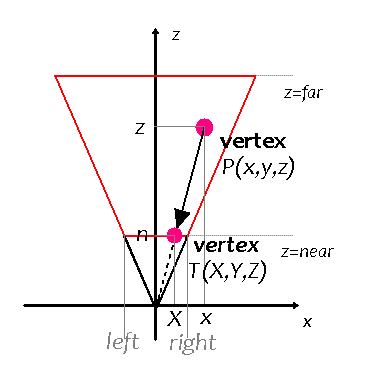
절두체공간의 xz 평면[y축에서 카메라의 시야 영역을 봤을 때]위에 정점P가 위의 그림처럼 위치한다고 할 때,
점P를 z=near 상에 투영시킬 때 투영된 점T의 x좌표가 투영변환 된 점Q의 X이다. 투영된 점 T의 X 좌표는 닮음비를 이용해서 구하면
투영변환에 의해 정점이 이동되는 공간은 (-1,-1,0)~(1,1,1)의 공간이므로, [-1,1]로 범위를 조정하는 계산을 추가로 해준다.
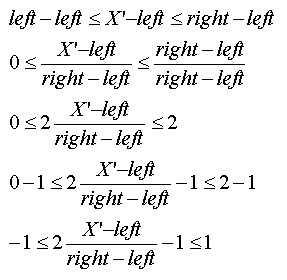
따라서, X 는 아래와 같다.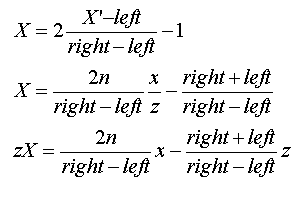
위의 수식중, 중간의 식이 최종변환된 X의 수식이고, [마지막의 식은 나중에 행렬을 구할 때 계산 편의상 X에 z를 곱해둔식이다.] 마찬가지로 y에서 Y로의 변환은 아래와 같다.
마지막으로, z에서 Z로의 변환을 보면, z의 변환의 경우 x,y의 변환과는 계산과정이 다르다.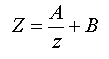
위와같은 형식으로 Z를 가정할 때,
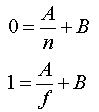
z가 n[near] 일경우 변환된 Z는 0 이고, z가 f[far] 일 경우 변환된 Z는 1 이 될것이다.따라서, A와 B를 구하여 대입하면
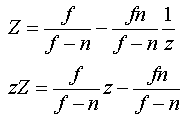
위와같은 결과를 얻을 수 있다.

이제, (x, y, z, 1) 이 (zX, zY, zZ, z) 로 변환되도록 행렬을 구성하면,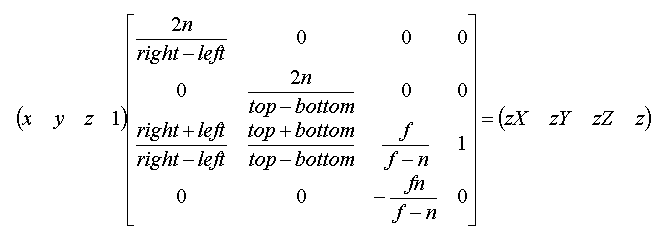
이 때, right = - left 이고, top = - bottom 이므로, 행렬의 (3,1)성분과 (3,2)성분이 0 이 된다. 또, right-left = Width, top - bottom = Height 로 정의하면, 최종 투영변환행렬이 아래와 같이 구해진다.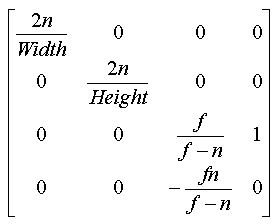
'이러저런 이야기' 카테고리의 다른 글
정수만 사용해서 선 빠르게 그리기 (0) 2019.12.19 왼손 좌표계 오른손 좌표계 (0) 2019.12.19 점이 삼각형 내부에 있는지 외부에 있는지 판별 (1) 2019.12.19 백스페이스 컬링 (0) 2019.12.19 벡터의 내적과 외적을 응용해 왼쪽 오른쪽 판별 (0) 2019.12.19