벡터의 내적 공식 유도하기

벡터의 내적이란?

두 벡터의 내적 결과 값은 스칼라 값이 나오며 세타 값은 두 벡터 사이의 각을 뜻 합니다. 그래픽스에서는 이 세타 값이 0인지 아닌지만 기억하시면 됩니다. [0이면 두 벡터는 직교한다.]

두 벡터의 내적의 공식 유도를 하기 전에 제1 코사인 법칙과 제2 코사인 법칙을 설명하겠습니다.

먼저 제1 코사인 법칙은 위와 같은 그림의 삼각형이 있을 때 각 꼭짓점에서 마주 보는 선분을 a, b, c라고 했을 때 각 선분의 길이는 아래와 같습니다.

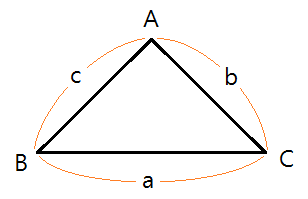
제1 코사인 법칙

왜 이렇게 되는지 유도를 해보자면 선분 a[BC] 의 길이는 선분 Ba +  선분 Ca 라고 할 수 있습니다. 위 식에서 보이는 [b * cos C]에서 cos C는 코사인 법칙으로 Ca / b라 할 수 있습니다. 따라서 [b * cos C = 선분 Ca]가 나오게 됩니다.  [c * cos B]도 마찬가지로 코사인 법칙으로 Ba / c 이며, 결국 [c * cos B = 선분 Ba]가 됩니다. 다른 선분 b, c도 유도하면 같습니다.

다음으로 제2 코사인 법칙은 위와 같은 삼각형이 있을 때 다음 공식이 성립이 됩니다.

 

제2 코사인 법칙

이 공식을 유도할 때 제1 코사인 법칙이 사용됩니다.

1. 제1 코사인 법칙인 a = bcosC + ccosB에 a를 곱해주고 두 번째 공식에는 b를 세 번째 공식에는 c를 곱해줍니다.

 

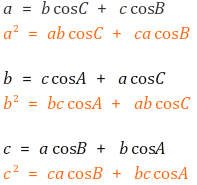
2. 변형된 식을 다음과 같이 만들어 빼줍니다.

위 식에서 a^2 - b^2를 먼저 풀어 줍니다.

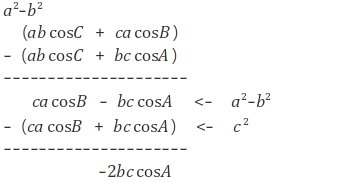
나온 값에 c제곱을 빼주면 -2bccosA가 나옵니다.

 

3. a2을 기준으로 이항 해줍니다.

다른 식도 다음과 같이 유도를 진행하면 됩니다.

 

벡터의 내적은 a의 성분을 (x1, y1, z1)라 하고 b의 성분을 (x2, y2, z1 )라 하면 내적은 a·b = x1*x2 + y1*y2 + z1*z2입니다. 또 다른 공식으로는 a·b = ||a|| ||b|| cos θ입니다. x1*x2 + y1*y2 + z1*z2 = ||a|| ||b|| cosθ이 공식이 성립이 된다는 뜻입니다.

그렇다면 여기서 아래와 같은 벡터 A와 B가 있을 때,

제2코사인 법칙을 이용해서 나타내 주면 다음과 같습니다.

제2 코사인 법칙에서 보던 그림과 같습니다. 그다음에 각각 선분의 크기를 구해주면 아래와 같습니다.

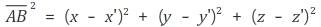
선분 AB의 크기

선분 OA의 크기

선분 OB의 크기

 

 

| 첫 번째 결과식

에서 선분[OA] 와 선분[OB]를 없애기 위해 아래와 같이 해줍니다.

계산한 결과 (1)의 결과를 얻을 수 있습니다.

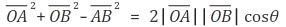
결과(1)

 

 

| 두 번째 결과식

각 벡터의 내적(원소들끼리 곱하고 더한 값)을 계산해보겠습니다.

위에서 구한 각 선분들 크기를 대입해주고 풀어주면 아래와 같이 나옵니다.

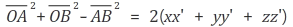
결과(2)

 

아까 (1)식과 (2)식을 비교해보면

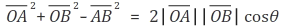
 결과(1)

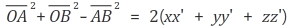
결과(2)

아까 벡터의 내적 공식에서  x1*x2 + y1*y2 + z1*z2 = ||a|| ||b|| cosθ이 공식이 성립 된다는 것을 볼 수 있습니다.